ΝΟΜΟΣ ΤΟΥ Bendford
1 Ιστορικό
Το 1881 o αστρονόμος και μαθηματικός Simon Newcomb έκανε μια αξιοσημείωτη παρατήρηση στους λογαριθμικούς πίνακες που χρησιμοποιούσε. Την εποχή εκείνη όλοι οι υπολογισμοί γίνονταν με το χέρι. Συχνά, για πολύπλοκες αριθμητικές παραστάσεις χρησιμοποιούνταν ως βοηθήματα οι λεγόμενοι λογαριθμικοί πίνακες - υπήρχαν μάλιστα βιβλία με ατέλειωτες σελίδες από αυτούς. Παρατήρησε λοιπόν ότι οι σελίδες του βιβλίου λογαρίθμων με αριθμούς που ξεκινούσαν με 1, ήταν περισσότερο φθαρμένες από τις υπόλοιπες. Αμέσως του παρακινήθηκε η περιέργεια και άρχισε να μελετά κι άλλα σύνολα δεδομένων, τα οποία προέρχονταν από διάφορες φυσικές διαδικασίες και συστήματα. Μετά από αρκετή έρευνα ο Newcomb συμπέρανε αυτό που αργότερα ονομάστηκε ως νόμος του Benford: τα σημαντικά ψηφία των αριθμών των διαφόρων φυσικών δεδομένων δεν κατανέμονται ισοπίθανα, αλλά ευνοούνται οι μικρότεροι αριθμοί.
Το 1938 ο φυσικός Frank Benford έκανε την ίδια ανακάλυψη με τον Newcomb. Ωστόσο ο Benford προχώρησε παραπέρα και μελέτησε πολλά περισσότερα σύνολα δεδομένων - συγκεκριμένα γύρω στα 20.229. Μεταξύ άλλων, τα δεδομένα του Benford προέρχονταν από αριθμούς σελίδων σε άρθρα περιοδικών, από συνολικά μήκη ποταμών κι από στατιστικά αγώνων baseball. Σε αντίθεση με τον Newcomb, η εργασία του Benford αναγνωρίστηκε και ονομάστηκε Νόμος του Benford, προς τιμήν του.
2 Ισχύς και περιορισμοί
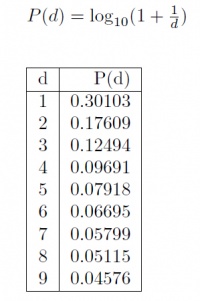
Ο νόμος ισχύει ανεξάρτητα από το σύστημα αρίθμησης (π.χ., δυαδικό, δεκαδικό, δεκαεξαδικό κ.ά.) που είναι εκφρασμένοι οι αριθμοί του υπό μελέτη συνόλου δεδομένων. Για τους συνήθεις αριθμούς στο δεκαδικό σύστημα, δηλαδή για τους αριθμούς που εκφράζονται με συνδυασμό των ψηφίων από 0 έως 9, ο Benford απέδειξε ότι η πιθανότητα το πρώτο σημαντικό ψηφίο να είναι 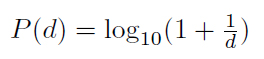 .
.
Ο νόμος του Benford δοκιμάστηκε και επαληθεύθηκε σε αριθμητικά δεδομένα που προκύπτουν από διάφορα φυσικά, οικονομικά και κοινωνικά συστήματα, όπως χρόνοι ημιζωής για άλφα και βήτα διασπάσεις, ατομικά φάσματα, τιμές μετοχών, αριθμοί λογαριασμών, ποσοστά θνησιμότητας, διευθύνσεις οδών, αριθμοί άρθρων σε εφημερίδες, πληθυσμοί χωριών και πόλεων, μαθηματικές σταθερές, μήκη ποταμών κ.ά.
Ο νόμος του Benford δεν έχει καθολική ισχύ. Διαπιστωμένα δεν ισχύει για αριθμούς που προκύπτουν από πραγματικά τυχαίες διαδικασίες. Σε μια πραγματικά τυχαία ακολουθία αριθμών η πιθανότητα εμφάνισης ενός εκ των 1 έως 9 στη θέση του πρώτου σημαντικού ψηφίου είναι η ίδια, δηλαδή 1 προς 9.
Δεν ισχύει επίσης για αριθμούς από μικρά σύνολα δεδομένων. Κατά κανόνα, όσο μεγαλύτερο το εύρος και το πλήθος των δεδομένων, τόσο με μεγαλύτερη ακρίβεια ισχύει ο νόμος του Benford.
Για παράδειγμα, μπορεί κανείς να αναμένει ότι ο νόμος του Benford θα εφαρμοστεί σε έναν κατάλογο αριθμών που αντιπροσωπεύουν τους πληθυσμούς των βρετανικών οικισμών ή αντιπροσωπεύει τις αξίες μικρών ασφαλιστικών απαιτήσεων. Αλλά αν ένα "χωριό" ορίζεται ως οικισμός με πληθυσμό μεταξύ 300 και 999, ή μια "μικρή ασφαλιστική απαίτηση" ορίζεται ως απαίτηση μεταξύ $ 50 και $ 99, τότε ο νόμος του Benford δεν ισχύει.
3 Εφαρμογές
Το 1972, ο καθηγητής Hal Varian του Information School στο Berkley, πρότεινε να χρησιμοποιηθεί ο νόμος του Benford για τον ευκολότερο εντοπισμό ψευδών φορολογικών δηλώσεων, με βάση το σκεπτικό ότι όσοι τις κάνουν τείνουν να κατανέμουν τα σχετικά νούμερα με τυχαίο τρόπο, αποκλίνοντας έτσι σημαντικά από την κατανομή Benford.
Σήμερα ο νόμος του Benford θεωρείται ένα πολύ ισχυρό εργαλείο για τον εντοπισμό λογιστικών ατασθαλιών, καταχρήσεων, φοροδιαφυγής κλπ. Η λογική είναι ότι αν κάποιος προσπαθήσει να παράξει ένα σύνολο από τυχαία δεδομένα, τότε προσπαθεί να τα κάνει κατά το δυνατό ομοιόμορφα, διότι θεωρεί ότι αυτό δείχνει μεγαλύτερη τυχαιότητα. Στην πραγματικότητα όμως για πραγματικά δεδομένα πολύ συχνά ισχύει ο νόμος του Benford.
Στις Ηνωμένες Πολιτείες, αποδεικτικά στοιχεία βασισμένα στον νόμο του Benford, έχουν κατατεθεί σε ομοσπονδιακά, κρατικά και τοπικά δικαστήρια.
4 Πηγές
- https://deltahacker.gr/aprosmeni-pagida-gia-tous-forofigades/
- http://zenzizenzizenzics.blogspot.gr/2011/02/benford_3676.html
- http://datagenetics.com/blog/march52012/index.html
- https://www.wiley.com/en-us/Benford%27s+Law%3A+Applications+for+Forensic+Accounting%2C+Auditing%2C+and+Fraud+Detection-p-9781118152850
- https://en.wikipedia.org/wiki/Benford%27s_law